Mittelwertsatz
Satz (Rolle)
Sei \([a, b]\) ein kompaktes Intervall mit \(a < b\) und \(f: [a, b] \mapsto \mathbb{R}\) eine stetige Funktion, die auf dem offenen Intervall \((a, b)\) differenzierbar ist. Falls \(f(a) = f(b)\) ist, so existiert ein \(\xi \in (a, b)\) sodass \(f'(\xi) = 0\).
Beweis (Rolle)
Nach dem Extremwertsatz werden Maximum und Minimum von \(f\) auf \([a, b]\) angenommen. Das heißt, es existieren \(x_{min}, x_{max} \in [a, b]\) mit:
\[f(x_{min}) = min(f([a, b])),\;\;\;\;\;\;\;\;\;\;f(x_{max}) = max(f([a, b])).\]Die Ableitung von \(f\) muss in allen Punkten \((a, b)\), wo ein Extremum angenommen wird, Null sein. Falls also \(x_{min} \in (a,b)\) oder \(x_{max} \in (a,b)\) gilt, dann haben wir bereits ein \(\xi \in (a,b)\) gefunden mit \(f'(\xi) = 0\) (wobei \(\xi = x_{min}\) oder \(\xi = x_{max}\) ist). Falls aber \(x_{min}\) oder \(x_{max}\) Endpunkte des Intervalles sind, dann muss wegen \(f(a) = f(b)\) auch \(f(x_{min}) = f(x_{max})\) gelten, womit die Funktion \(f\) einfach konstant ist und \(f'(x) = 0\) für alle \(x \in (a,b)\) gilt. \(\square\)
Satz (Mittelwertsatz)
Sei \([a,b]\) ein kompaktes Intervall mit \(a < b\) und \(f: [a,b] \mapsto \mathbb{R}\) eine stetige Funktion, welche auf dem offenen Intervall \((a,b)\) differenzierbar ist. Dann gibt \(\xi \in [a,b]\) mit:
\[f'(\xi) = \frac{f(b) - f(a)}{b - a}.\]Beweis (Mittelwertsatz)
Wir definieren eine Funktion \(F:[a, b] \mapsto \mathbb{R}\) durch
\[F(x) = f(x) - \frac{f(b)-f(a)}{b-a}(x-a)\]für alle \(x \in [a,b]\). Dann gilt \(F(b) = f(b)-(f(b)-f(a)) = f(a)\).
Des Weiteren ist \(F\) stetig an den Endpunkten und differenzierbar auf \((a,b)\). Nach dem Satz von Rolle existiert also ein \(\xi \in (a,b)\) so dass
\[0 = F'(\xi) = f'(\xi)-\frac{f(b)-f(a)}{b-a}\]wie gewünscht. \(\square\)
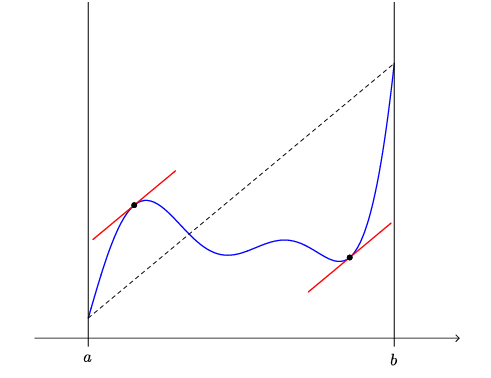
Bild (Mittelwertsatz)