Zwischenwertsatz

Satz (Zwischenwertsatz)

Sei \(I \subseteq \mathbb{R}\) ein Intervall, \(f: I \rightarrow \mathbb{R}\) eine stetige Funktion und \(a, b \in I\). Für jedes \(c \in \mathbb{R}\) zwischen \(f(a)\) und \(f(b)\) gibt es ein \(x_{0} \in \mathbb{R}\) zwischen \(a\) und \(b\), so dass \(f(x_{0}) = c\) gilt.

Beweis (Zwischenwertsatz)

Wir nehmen ohne Beschränkung der Allgemeinheit an, dass \(a < b\) und \(f(a) \le f(b)\) gilt (falls \(f(a) \ge f(b)\)), betrachtet man \(-f\) ). Sei nun \(c \in [f(a), f(b)]\). Falls \(c = f(a)\) oder \(c = f(b)\) gilt, sind wir fertig. Also angenommen \(c \in (f(a), f(b))\). Wir definieren

\[ X = \{x \in [a,:b]\;|\;f(x) \le c \}\]

und bemerken, dass \(a \in X\) und \(X \subseteq [a, b]\), wodurch X nicht-leer und von oben beschränkt ist. Mit dem Satz über die Existenz des Supremums existiert daher \(x_{0} = sup(X) \in [a, b]\).

Wir verwenden nun die Stetigkeit von \(f\) bei \(x_{0}\), um zu zeigen, dass \(f(x_{0}) = c\). Für jedes \(\epsilon > 0\) gibt es ein \(\delta > 0\), so dass für alle \(x \in [a, b]\) gilt:

\[|x - x_{0}| < \delta \implies |f(x) - f(x_{0})| < \epsilon\]

1. Angenommen \(f(x_{0}) < c\). Dann folgt \(x_{0} < b\) wegen \(f(b) < c\) und \(x_{0} \in [a, b]\). Wir wenden nun die Stetigkeit von \(f\) bei \(x_{0}\) an und finden für \(\epsilon = c - f(x_{0}) > 0\) ein \(\delta > 0\), dass die Stetigkeits-Definition von vorhin erfüllt. Da nun \(x_{0} < b\) ist, existiert ein \(x \in (x_{0}, x_{0} + \delta) \cap [a ,b]\). Für dieses \(x\) gilt dann:

\[f(x) = f(x_{0}) + (f(x) - f(x_{0})) < f(x_{0}) + c - f(x_{0}) = c\]

Also muss \(x\) in \(X\) liegen, was aber \(sup(X) = x_{0} < x\) widerspricht.

2. Angenommen \(f(x_{0}) > c\). Dann folgt \(x_{0} > a\) wegen wegen \(f_{a} < c\). Wir verwenden erneut die Stetigkeit von \(f\) bei \(x_{0}\) und finden für \(\epsilon = f(x_{0}) - c\) ein \(\delta > 0\), dass die Stetigkeits-Definition von vorhin erfüllt. Für \(x \in (x_{0} - \delta, x_{0}) \cap [a ,b]\) gilt dadurch

\[f(x) = f(x_{0}) + (f(x) - f(x_{0})) > f(x_{0}) - (f(x_{0})) - c) = c.\]

wodurch \(x \notin X\) und daher \((x_{0} - \delta, x_{0}) \cap [a, b] \cap X = \varnothing\). Also ist \(x - \delta\) eine obere Schranke von \(X\), was aber \(x_{0} = sup(X)\) widerspricht. Daher gilt \(f(x_{0}) = c\) und der Satz folgt. \(\square\)

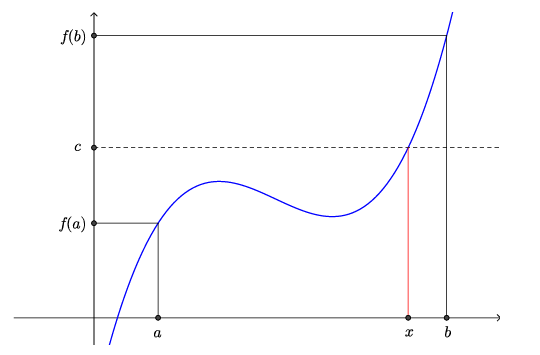
Bild (Zwischenwertsatz)